交点の位置ベクトルを天びん法を使って解く

[mathjax]
交点の位置ベクトルの問題
数Bのベクトルの単元で習う問題
こんなやつ
△OABにおいて, 辺OAを3:2に内分する点をM, 辺OBを3:4に内分する点をN, 線分ANとBMの交点をPとする。
\(\overrightarrow{OP}\)を\(\overrightarrow{OA}\)=\(\vec{a}\), \(\overrightarrow{OB}\)=\(\vec{b}\)を用いて表わせ
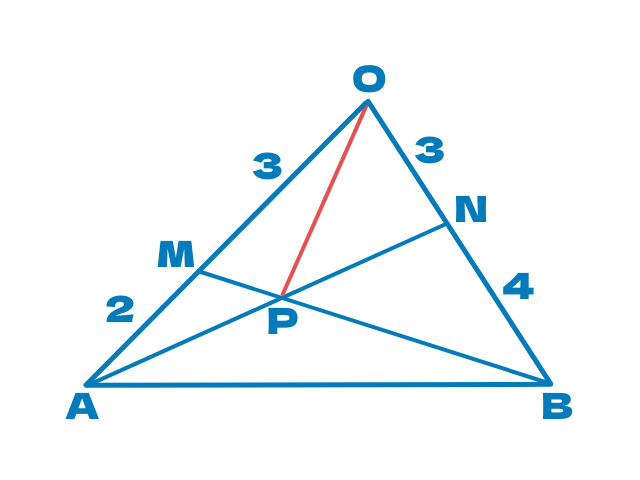
かなりよく見る問題ですね
これを\(s\)とか\(t\)とか使わないで
連立方程式も使わないで
メネラウスの定理も使わないで
天びん法の力を使って解く
その方法をご紹介
[outline]
天びん法をマスターする
まずは天びん法から話をしていきましょう
中学受験経験者は知っているかもしれませんね
食塩水の問題をやったときに
習ったことがあると思いますので
とりあえず図を1つ
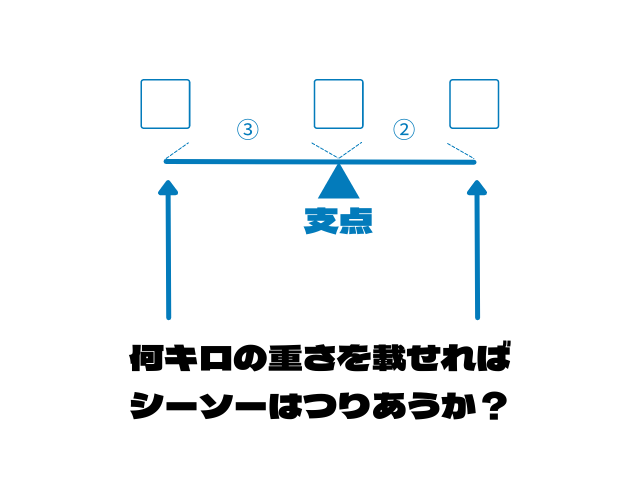
支点を境に左右の長さの比が3:2になっているシーソーがあると思ってください
ちょうど釣り合わせるためには
左と右それぞれ何キロの重さを載せればいいのか?
答えいっちゃいますね
長さの比と重さの比を逆にするとつりあいます
逆比っていうんですが
長さが3:2なので重さの比を2:3にしてあげればOKです
こんな感じです
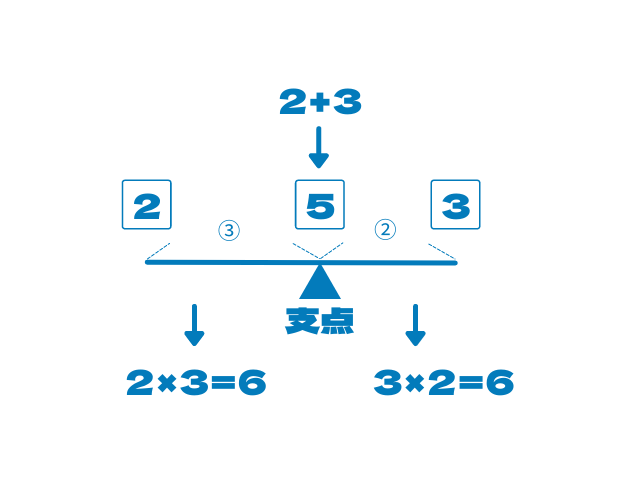
このとき
支点には2+3で5の重さがかかっています
これも覚えておいてください
あとで使います
それから
左側の重さの比と長さの比をかけたものは
右側の重さの比と長さの比をかけたものと等しくなる
これも追加でお願いします(;・∀・)
左は2×3=6
右は3×2=6
どちらも同じ数字になっていますね
連比の考え方をマスターする
続いて連比の話
こちらも実は中学受験で習う内容です
連比の知識も必要なので説明しておきます
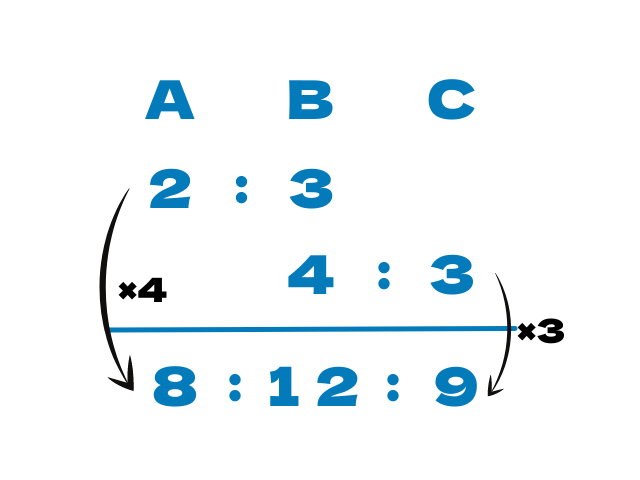
例えばA:Bが2:3
B:Cが4:3だとします
ではA:B:Cはいくつでしょう?という問題
こちらも図で解説
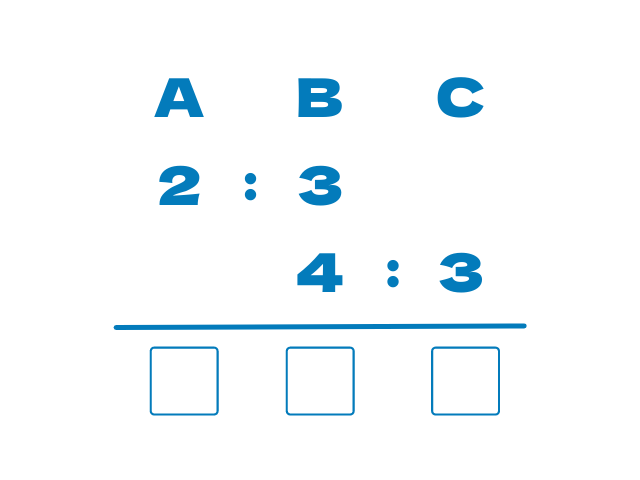
上と下でBの比が違うので揃えてあげる必要があります
つまり同じ数字にすればいいんですね
3と4を同じ数字にする・・・
最小公倍数を出してあげてください
3と4の最小公倍数は12
ということでBは12になりました
これで終わり・・・ではありません( ;∀;)
3を12にするのに4倍していますので
Aの2も4倍します=8
4を12にするのに3倍していますので
Cの3も3倍します=9
こんな感じですね
最終的な答えは8:12:9となります
これが連比の考え方です
交点の位置ベクトル問題を解く
さてこれで準備は整いました
では解いていきましょう
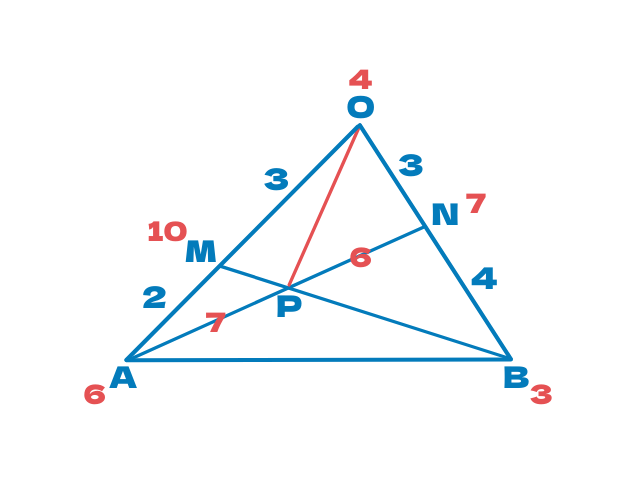
もう1度あの図を

先ほどの天びん法を使って
残りの辺の比を出していきましょう
AP:PNの比さえ出てしまえばあとは簡単ですからね
辺OAと辺OBから出していきます
できました
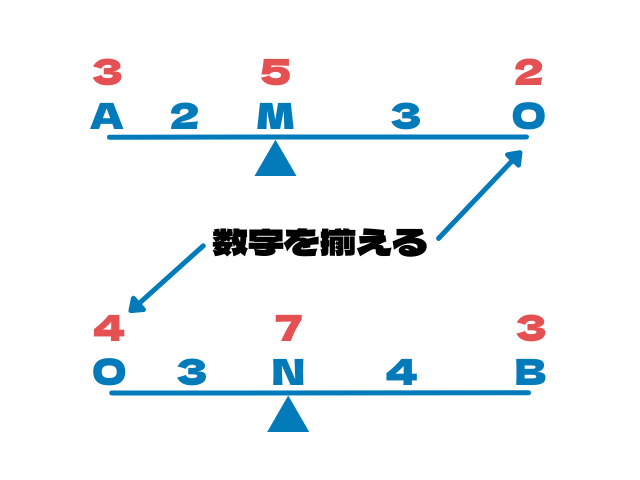
でもこのままだと点Oの数字が「2」と「4」で異なります
ここで連比の登場
最小公倍数で揃えてあげましょう
上の段の数字をすべて2倍すればOK
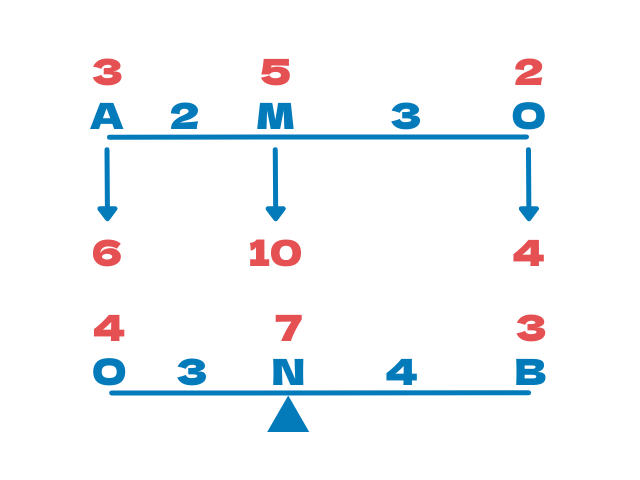
はい
これで揃いました
最初の図に転記していきます
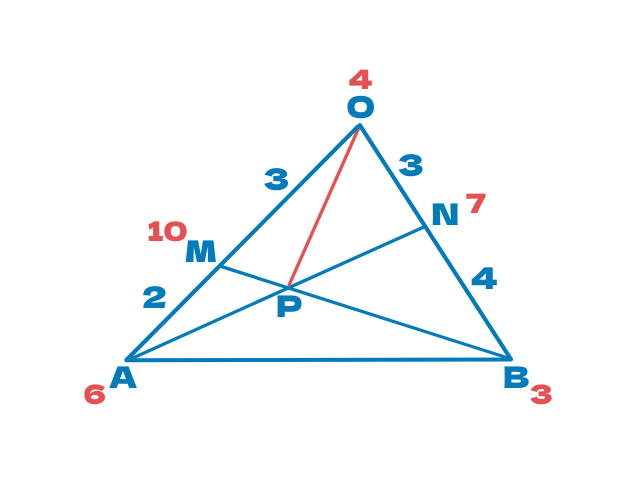
はい、どうでしょう
ここまでくればAP:PNの比もわかりますね
天びん法を使って
逆比にすればいいので
7:6になるとわかります
ここまできたらゴールはすぐそこ
内分点の位置ベクトルの公式を使って計算していきましょう
公式は・・・
$$\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}$$
使う三角形はここ
緑の三角形です
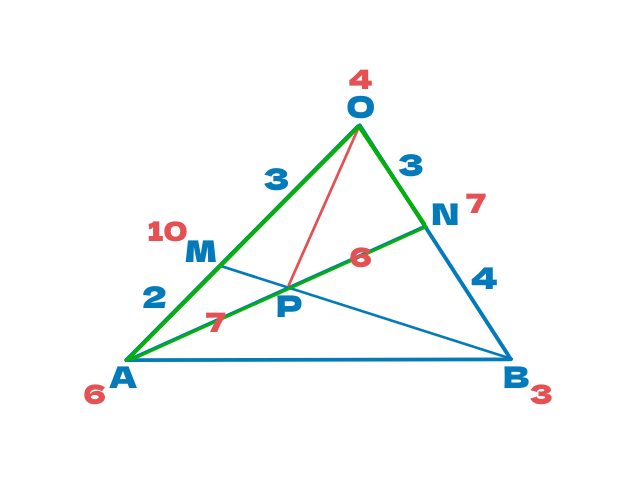
$$\overrightarrow{OP}=\frac{6\overrightarrow{OA}+7\overrightarrow{ON}}{7+6}$$
$$=\frac{6}{13}\overrightarrow{OA}+\frac{7}{13}×\frac{3}{7}\overrightarrow{OB}$$
$$=\frac{6}{13}\overrightarrow{OA}+\frac{3}{13}\overrightarrow{OB}$$
$$=\frac{6}{13}\overrightarrow{a}+\frac{3}{13}\overrightarrow{b}$$
解けました!
ふーーー
ここまで書くの大変だった・・・

