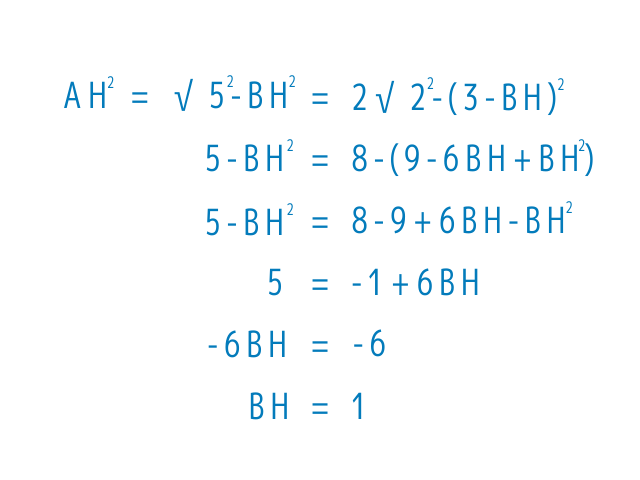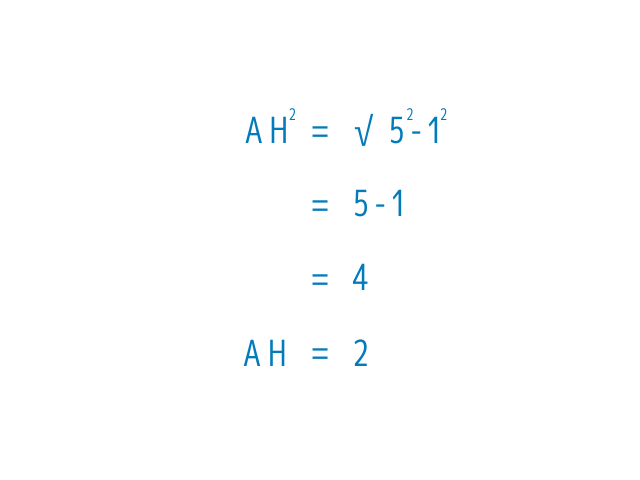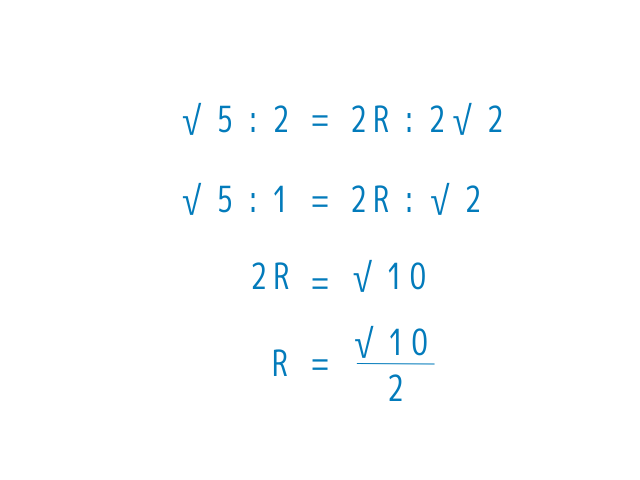外接円の半径の求め方（高校入試対策）

外接円の半径・・・

高校で出し方は習うけど

中学でやったかな・・・

 

でも高校入試問題で見たことはあるので・・・(；・∀・)

解き方を説明していきますね

 

では早速問題です

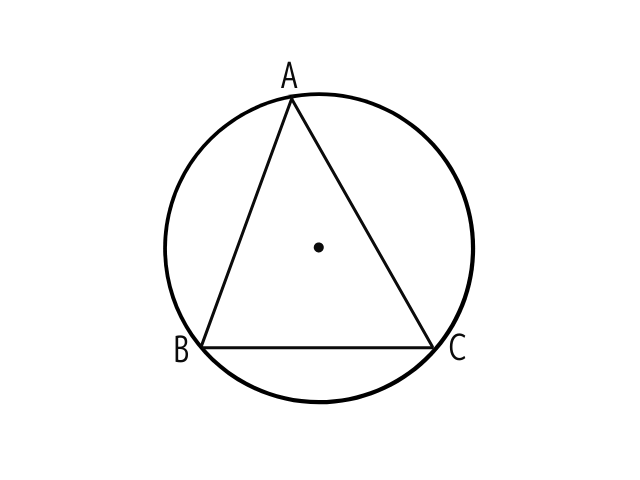
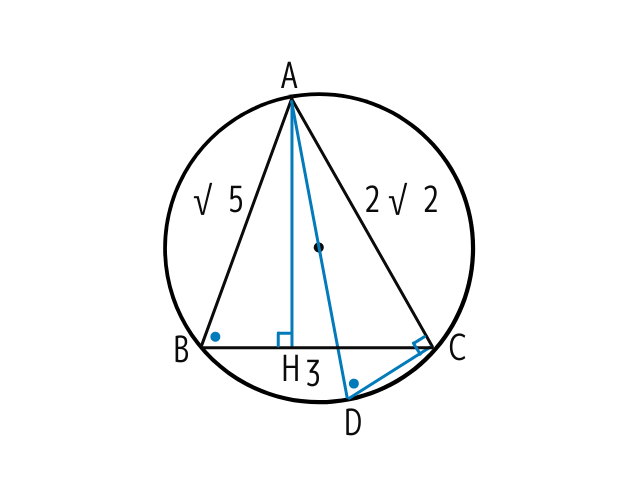
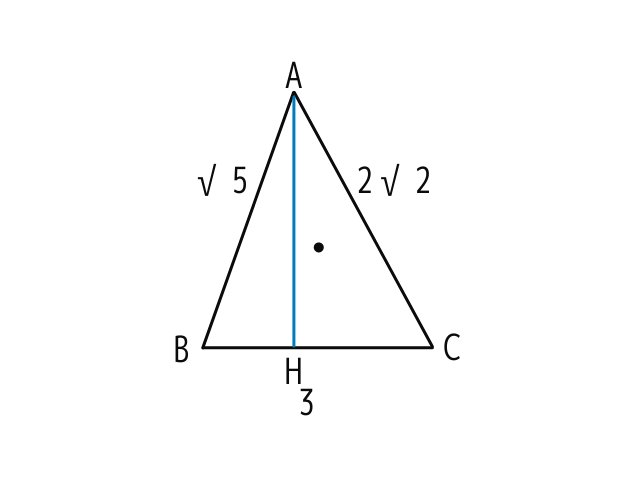
△ABCの３つの頂点は円Oの周上にあり、AB＝√５cm、BC＝３cm、CA＝２√２cmである。この三角形の半径を求めよ。

さていきますか

高校の知識を使わずに解く方法

 

解いてみたい方は

いったんスクロールを停止してくださいね

 

・

・

・

・

 

今回は「相似」と「三平方の定理」を使って解きます

あ、あと「円周角の定理」も

 

・

・

・

ではいきます

 

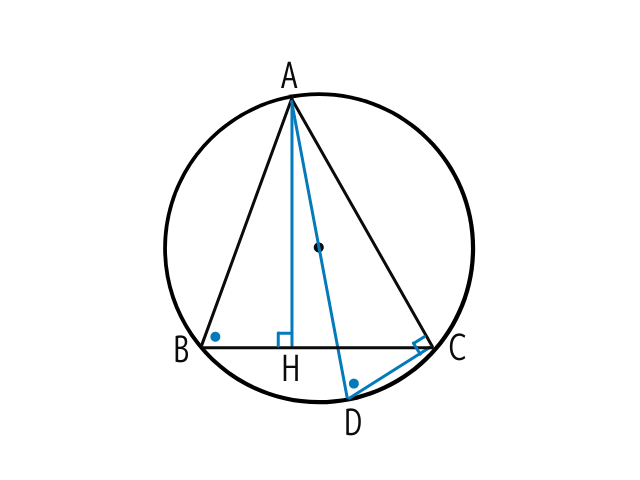
まずは補助線を引いて相似な三角形を作りましょう

1. AからBCに向かって垂直な線を引き交点をHとします
2. Aから中心を通る直線（直径）を引き円周との交点をDとします
3. DとCを結びます

こんな感じになりましたか？

∠AHBは９０度

∠ACEも円周角の定理から９０度

 

○印がついている

∠Bと∠Dはこちらも同じ弧（AC）に対する円周角は等しいので

同じ大きさとわかりますね

 

この時点で△ABHと△ADCは２組の角がそれぞれ等しいので

相似であることが確定

相似とわかれば

あとは比を使って半径を出したいところですが・・・

このままでは出せませんね〜

わからない長さが多すぎる・・・

 

底辺は使わないとして

AHは知りたいですね

 

では次の作業に移りましょう

AHを出していきますよ

 

今度は三平方の定理を利用します

一旦相似な三角形は横に置いておいて・・・

 

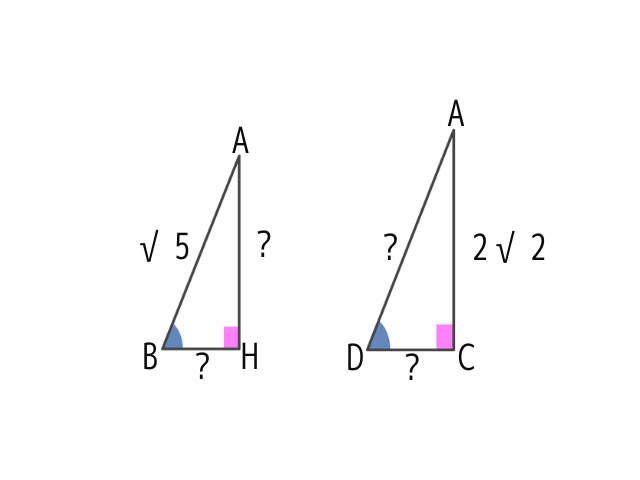
△ABCに注目

左の三角形と右の三角形に分けて考えてみましょう

三平方の定理を利用すると

こんな式ができます

実際の長さを代入してみましょう

まずはBHの長さが出ました

ここでさらに三平方を使って

AHを出していきましょう

出ました

AHの長さは２です

 

ゴールまであと少し

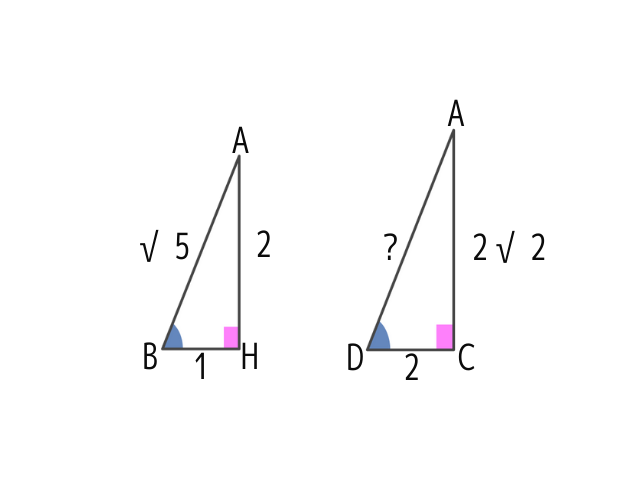
横に置いておいた相似な図形を再登場させましょう

さっきより

わかる長さが増えましたね〜

 

あとは比で出すだけ

半径をRとおくと

ADは直径なので２Rとおけます

答えがでました

R、つまり半径は√10 / 2です

 

ふー

少し長かったですね。。。

 

お疲れ様でした！