ディオファントス方程式を３つの方法で解く

[mathjax]

中学１年生の定期テストで出された文章問題

 

ディオファントスの墓

ディオファントスの一生

 

いろんな言い方はされていますが･･･

 

まずは問題をみてみましょう

 

 

さてこの問題どうやって解いていったらいいでしょう

 

あ！

問題とにらめっこしていても答えは浮かびませんよ

まずは手を動かして図を描いてみないと

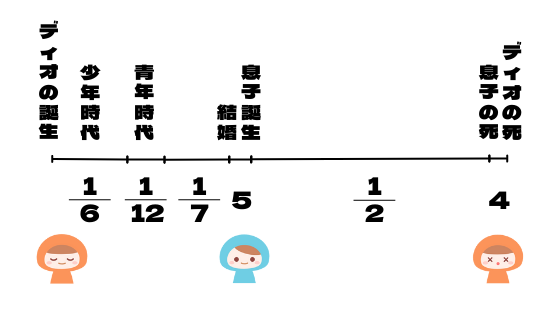
こんな感じでしょうか

それでは問題の解き方を解説していきます

 

[outline]

1次方程式を利用して解く

まずは１次方程式を利用して解く方法です

 

ディオファントスが亡くなった年を\(x\)歳として方程式を作ると･･･

$$\frac{1}{6}x+\frac{1}{12}x+\frac{1}{7}x+5+\frac{1}{2}x+4=x$$

となります

 

分数を整数にするために

両辺に最小公倍数の\(84\)をかけましょう

 

$$14x+7x+12x+420+42x+336=84x$$

$$-9x=-756$$

$$x=84$$

ということでディオファントスは\(84\)歳で亡くなったことがわかります

 

別の解き方

実はもう１つ別の解き方があります

わかってしまえばこっちのほうが簡単･･･かもしれません

 

例えばディオ君が\(100\)歳まで生きたとします

このうち\(\frac{1}{5}\)を少年として･･･と言われたら

\(100×\frac{1}{5}=20\)

少年時代が\(20\)年であることがわかりますよね

そんなに長いわけないじゃん！というクレームはなしで･･･

 

では例えば\(99\)歳まで生きたとしたらどうでしょう

\(99×\frac{1}{5}=19.8\)

\(19.8\)歳？

そんなことはないですよね

年齢なんですから計算結果は必ず整数になるはずです

 

ということは

\(\frac{1}{6}\)でも、\(\frac{1}{12}\)でも、\(\frac{1}{7}\)でも、\(\frac{1}{2}\)でも

どの数をかけても整数になる必要がある

割り切れる必要があるはずです

 

そう考えればこれら数字の公倍数が答えになるとわかります

最小公倍数は\(84\)

その次は\(168\)ですが、常識的にこの歳まで生きたとは考えられないので

答えは\(84\)歳だとわかります

 

方程式を使わないで解く方法

もう１ついってみましょう

方程式を使わないやり方

小学生に教えるときはこれかなと

もう１度あの絵を･･･

 

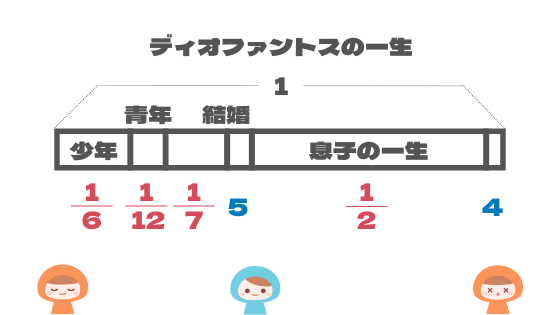
まずディオファントスの一生を1とおきます

次に分数の部分を全部足します

$$\frac{1}{6}+\frac{1}{12}+\frac{1}{7}+\frac{1}{2}$$

$$=\frac{14}{84}+\frac{7}{84}+\frac{12}{84}+\frac{42}{84}=\frac{75}{84}$$

この答えを先程の\(1\)からひきます

$$1-\frac{75}{84}=\frac{9}{84}$$

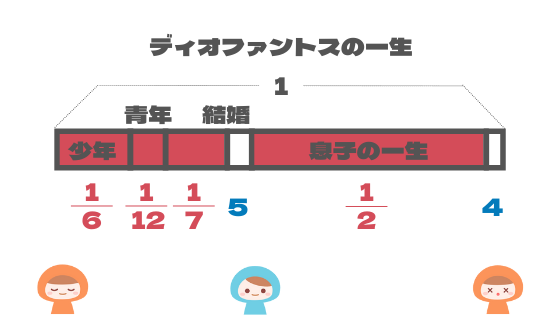
この\(\frac{9}{84}\)は\(5+4=9\)年にあたることがわかりますね

（グラフの白い部分）

 

ここまで出たらあと少し

比で出してしまいましょう

$$\frac{9}{84}:9=1:x$$

$$x=84$$

 

答えは\(84\)歳になります