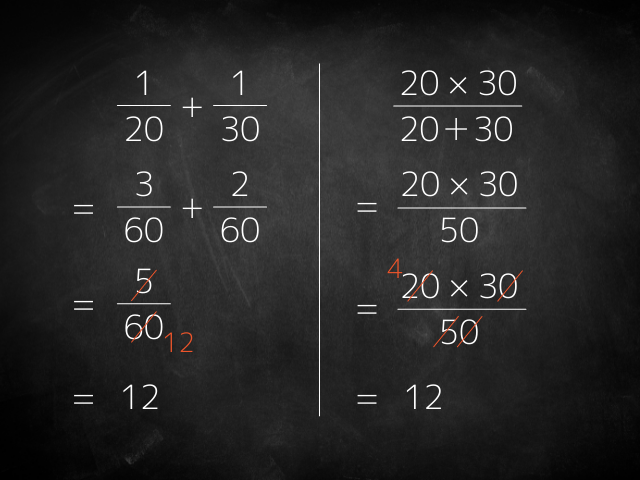並列の全体抵抗を簡単な計算で出す方法

中2理科【電流】
この単元の最初のほうに出てくる
オームの法則
電圧を出したり
電流を出したり
抵抗を出したり
その中の1つに
並列の全体抵抗を出す計算があるんですが
今年から公式をちゃんと習うんですよね・・・
去年まではなかったはずなんですが(;・∀・)
こんなやつです
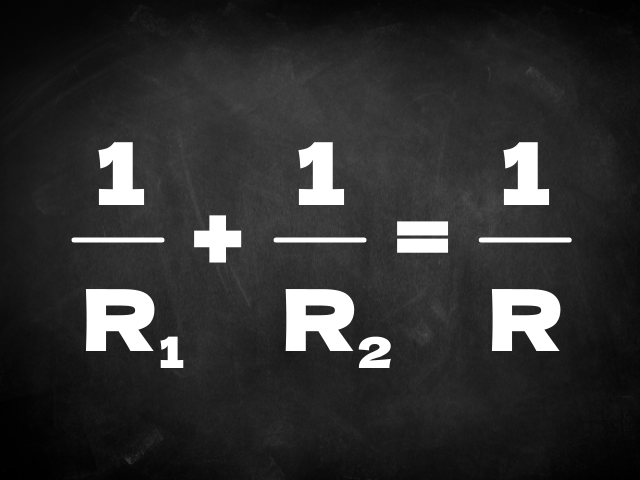
公式を使って普通に解く方法
1つ問題をやってみましょうか
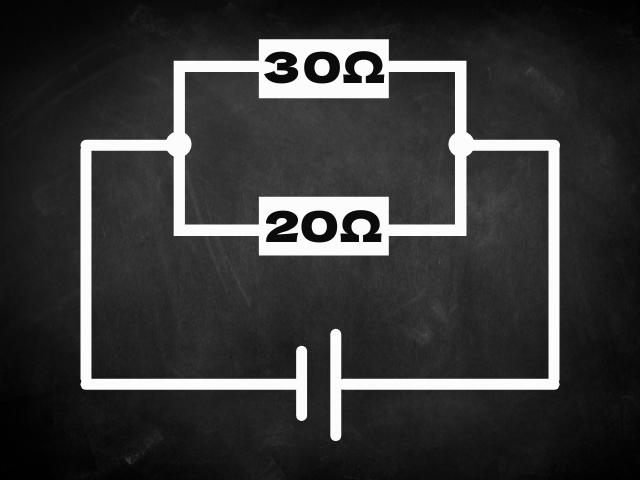
並列に繋がれた2つの抵抗がありますね
30Ωと20Ω
では上の公式を使って・・・
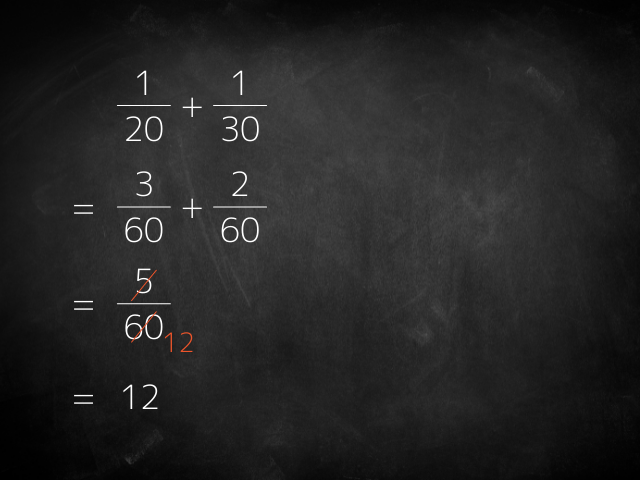
でました
12Ωです
数字がわかりやすいということもあって
通分がそれほど面倒ではないので
この数字の組み合わせならば
割とスムーズに解けそうです
ではこの計算を
別の方法を用いて解いてみましょう
和分の積の公式を使う
和分の積(わぶんのせき)の公式
数学でも使うことがあるんですが
こんなやつです
わぶんのせき
なんか言いたくなる公式ですね〜
分母が足し算の答え
分子が掛け算の答えです
では先程の問題をこの公式で解いてみましょう
和は20+30
積は20×30
なので・・・
左側はさっきのやつです
右側が和分の積を使ったバージョン
通分する必要がないので
その分計算は楽になりますね
逆数にする必要もないし
もちろん答えは同じ12です
あ、ちなみに・・・
この公式
抵抗が3つ並列しているときにも使えますが
3つ全部足してそれを分母にして・・・
3つ全部かけてそれを分子にして・・・
というやり方はできないので
そこだけお気をつけを・・・
たとえば
3Ω、6Ω、2Ωが並列になっていたとして

この計算方法では出せないということです
3つのときは
3と6の抵抗をまずだして
出た答えと残りの2との抵抗を出す
この流れであれば和分の積は使えます(下の図の左側)
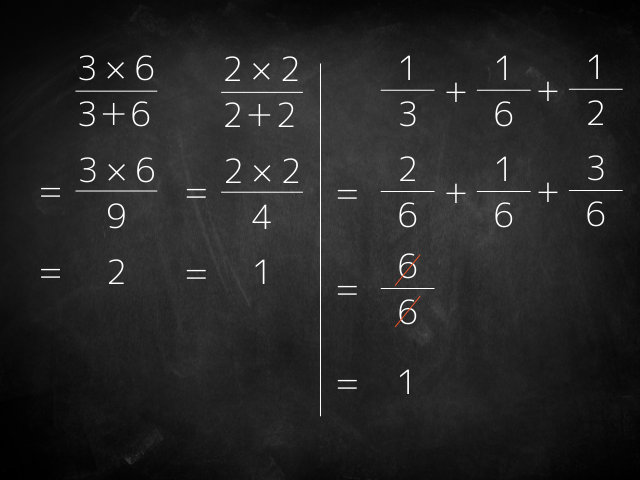
最もこの問題だと
普通に公式を使ったほうが速そうですが・・・(上の図の右側)
ではでは最後に
公式の証明?をして終わりにしましょう
和分の積の公式証明
2つの抵抗をaΩ、bΩとして
計算してみましょう
普通の公式を使ってときますよ
最後に和分の積の公式が登場しますので
みててください
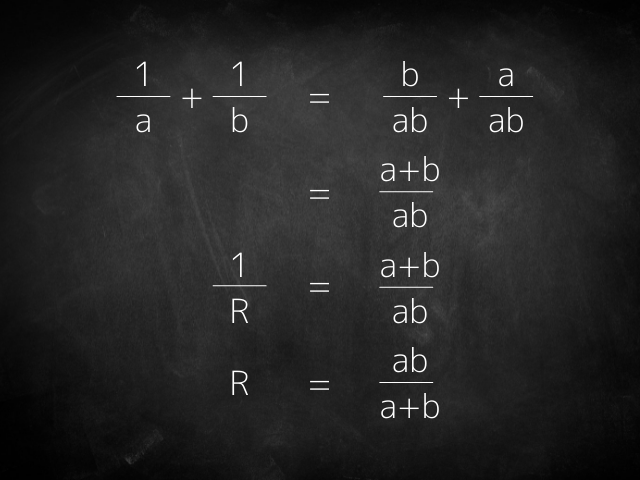
出ましたね
数字をaとbの文字に置き換えて
普通の公式を使ってとくと
あら不思議!!!
最後がちゃんと和分の積になっています!!
ということで今回はこの辺で終わりにしたいと思います!