最大公約数と最小公倍数の求め方[小・中・高バージョン]

[mathjax]

最小公倍数と最大公約数

この２つの求め方

実はいくつか種類がありまして

それを習う順に紹介していきたいと思います

 

それでは早速ですがいってみましょう！！

 

[outline]

小学校バージョン

一番最初に習う求め方

地道に数えていくスタイルですね

 

特に追加説明は･･･ないです(；・∀・)

中学受験バージョン

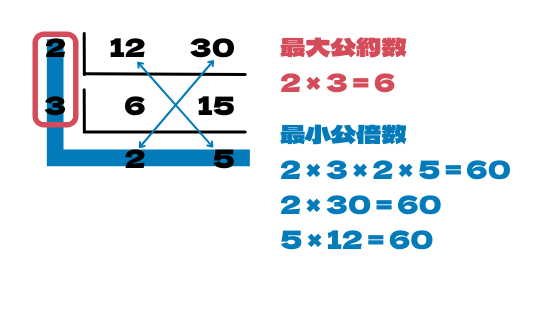
計算を使って求める方法

すだれ算でしたかね

正式名称は「連除法」

 

２つの数を素数で割っていき

あ、素数は小５で習いますよ

１以外の数字で割れなくなったらSTOP

 

左[赤丸]の数をかけた数が最大公約数

青で塗ってある数を全部かけた数が最小公倍数

 

もしくは青い矢印の先にある数字をかけても出せますね

 

ちなみに３個バージョンもあるんですが

こっちはちょっと注意が必要なんですよね

それはまた別の機会にでも･･･

中学生バージョン

素因数分解を利用して求める方法

素因数分解は･･･

中１で習いますね

今までは中３でしたけど

 

それぞれの共通因数をかけると最大公約数になって

それぞれの因数すべてをかけると最小公倍数になります

高校生バージョン

いよいよ最後です

といっても新しい方法を習うわけではないんですよね

 

最大公約数と最小公倍数の･･･

ん〜

ちょっと名前長くて面倒なので省略しますね

最大公約数はGreatest Common Measureで「G」

最小公倍数はLeast Common Multipleで「L」とさせてください

 

高校ではこのGとLの関係を公式化したものを習います

先程記載した連除法がわかればそこまで難しくはないですよ

 

自然数\(a, b\)の最大公約数を\(g\)、最小公倍数を\(l\)としたとき

互いに素な自然数\(a’, b’\)を使うと

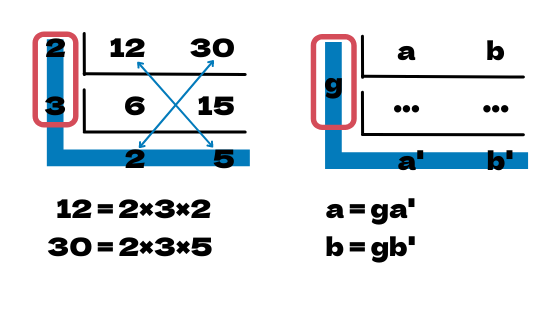
\(a = ga’\)

\(b = gb’\)

と表すことができます

このとき\(a’\)と\(b’\)は互いに素の関係ですね

 

さらに以下の式も成り立ちます

\(l = ga’b’\)

ここまでは連除法を文字化しただけなので大丈夫ですね

 

ラストもう１つ公式があります

\(ab = gl\)

自然数２つをかけると最小公倍数と最大公約数をかけたものと同じになる

というやつなんですが

 

なぜそうなるのか

理由を説明しておきましょう

\(a = ga’\)

\(b = gb’\)

\(ab = gga’b’ [ab = g･ga’b’]\)

\(l = ga’b’\)なので

\(ab = gl\)

とこんな感じです

 

これで終わりかな･･･

あ、しまった

アイツを忘れていた

 

すいません

もう１つだけ

「ユークリッドの互除法」というやつが残っていました

ユークリッドの互除法

数が大きいときに最大公約数を求める方法です

例えば６６７と２９９のGを求めなさいとか

 

連除法だと大変なんですよね

そんなときにコイツを使ってやってください

 

詳しい説明は省略します(；・∀・)

やり方だけ書いておきます

 

1. 小さい数字で大きい数字を割る
2. 余りで割る数を割る
3. これを割り切れるまで繰り返す
4. 最後の式の割る数が最大公約数

 

いや

これはもう

実際見たほうが早い

ということで

６６７と２９９の最大公約数（G）は２３ということになります

 

ふーーー

これで本当の本当に終わりです